计算机如何做加法

半加器与全加器

门电路是计算机硬件层面最基础的设计单元，计算机要想实现加法运算，也要利用这些门电路。

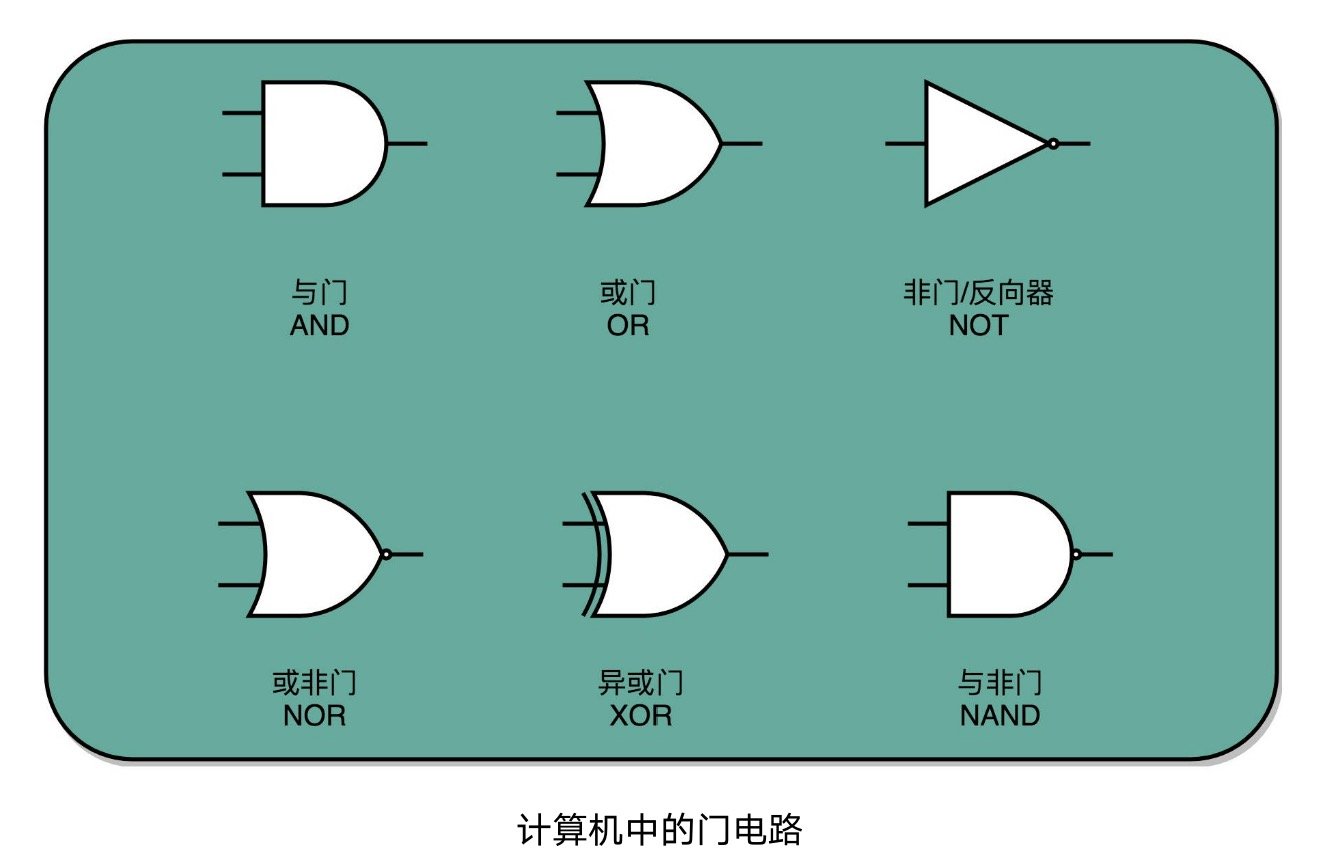
我们在做十进制的加法时，是逢十进一，同样的，在二进制的加法中，就是逢二进一。从下表中可以看出，两个 1 bit 位的二进制数相加的和等于这两个数做「异或」操作的结果，而产生的进位则等于这两个数做「与」操作的结果。

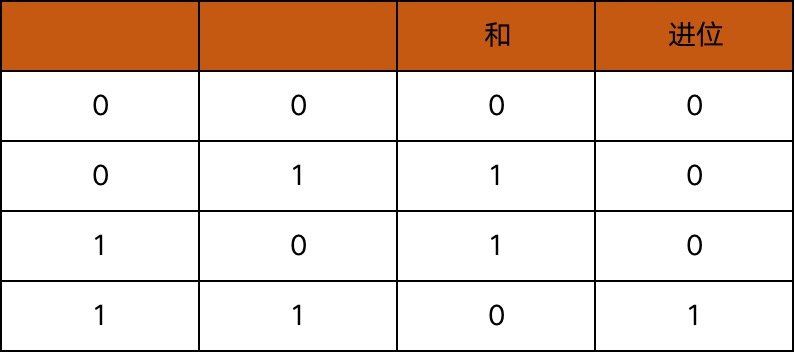
根据上述特点，可以很容易设计出下面这种电路，实现两个 1 bit 位的二进制数的加法。我们将这种电路称之为半加器。

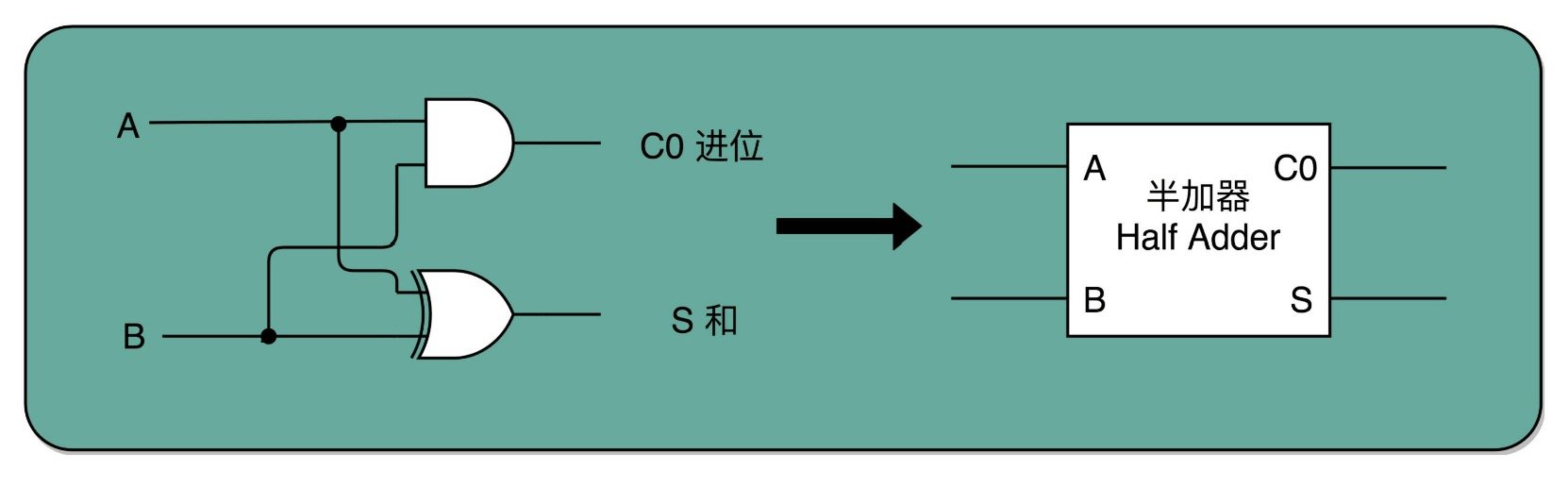
为什么叫半加器呢？因为这个电路只能计算两个 1 bit 位的二进制数的加法，一旦加数的位数变多了，半加器就用不了了。不过不用担心，两个半加器与一个或门组合，便可得到一个全加器，如下图所示。全加器能接收三个输入，分别是两个 1 bit 位的加数和一个进位信号，输出一个和以及一个进位，输出的这个进位可以作为下一个全加器的输入。虽然一个全加器也只能计算 1 bit 位的加法，但是，8 个全加器串联起来就可以实现两个 8 bit 位数的加法了，最后一个全加器的进位输出信号还可以作为是否溢出的标志位。

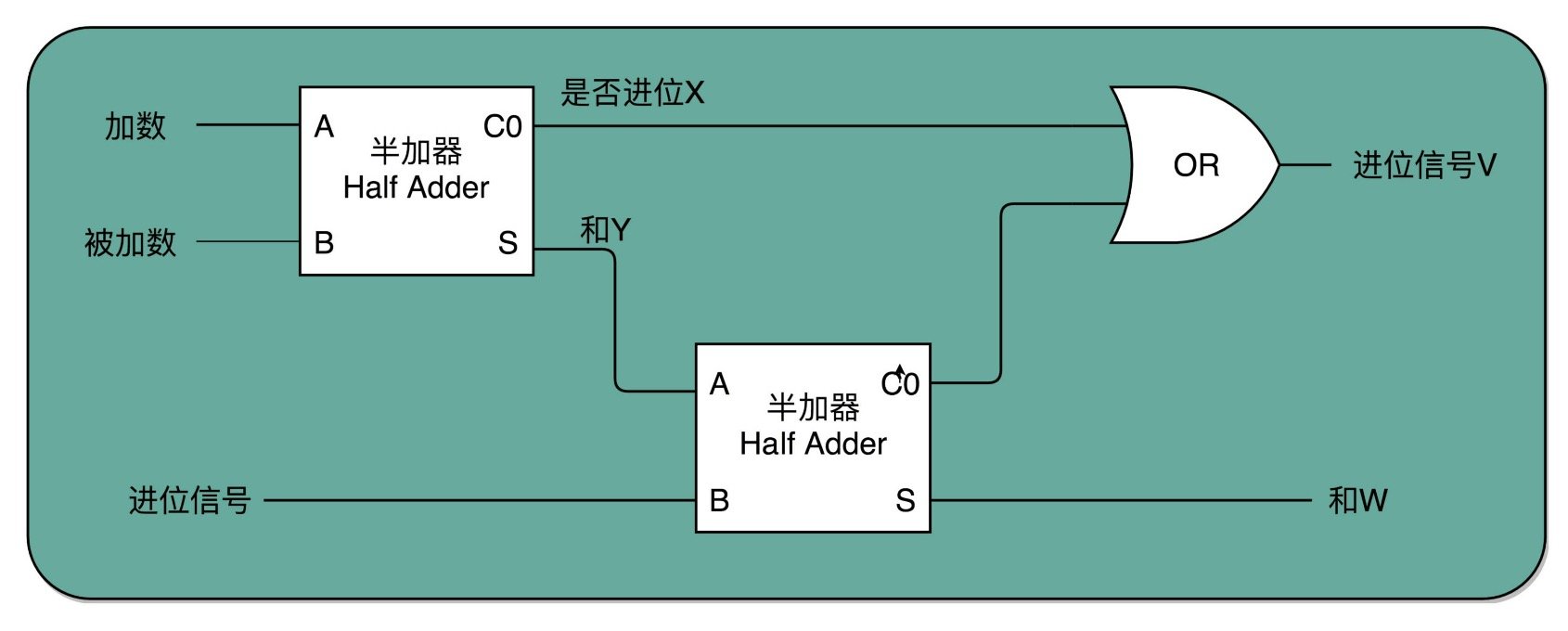
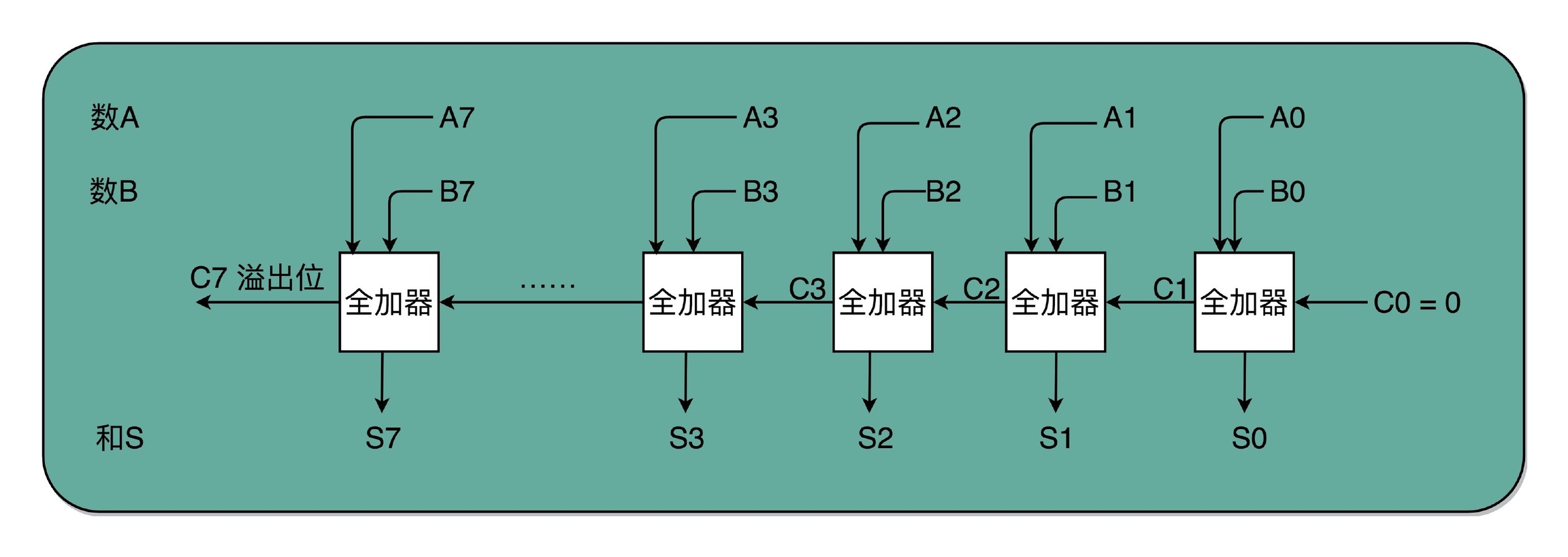
所以说，我们在做整数相加的运算时，判断结果是否溢出是得到了计算机硬件层面的支持的。

但是这样实现的全加器也有缺点，就是计算后一位的结果需要依赖前一位的输出，每一个全加器要从右往左依次进行运算，最左边的那个全加器要等他右边的全加器都计算完成后再进行计算。要知道，门电路工作是有时延的，专业术语叫做「门延迟」（Gate Delay），如果把门延迟的时间记为 T，那一个全加器计算进位就需要经历 3T，如果是 8 位的加法器，最高位的计算需要等待前面 7 个全加器的进位结果，也就是需要等待 21T 的门延迟。为了提高计算效率，查尔斯·巴贝奇等人设计了超前进位加法器，一定程度上解决了这个问题，现代 CPU 中普遍使用的都是超前进位加法器。

超前进位加法器

要想理解 CLA（Carry-Lookahead Adder，超前进位加法器）的原理，首先要知道两个概念：生成（generate） 和 传播（propagate）。生成和传播分别代表两种进位类型。

假设 A 和 B 是两个加数， $A_i$ 和 $B_i$ 分别代表 A 和 B 从右边数第 i 位上的数，i 从 0 开始计数， $C_i$ 代表第 i - 1 位产生的进位， $C_0=0$ 。生成指的是无论右边有没有进位，当前位上都会产生进位，比如二进制的 10 + 10，个位上相加得 0，二位（类似于十进制的十位）上相加得 0，产生进位 1，于是我们说二位上是生成的，我们用 $G_i$ 表示第 i 位是否生成，其实可以看出来，只有当 $A_i$ 和 $B_i$ 同时为 1 时，第 i 位才生成，所以 $G_i = A_i \cdot B_i$ （ $A_i \cdot B_i$ 表示 $A_i$ 和 $B_i$ 做「与」操作）；传播指的是由于右边有进位，导致当前位相加时产生了进位，比如二进制的 101 + 111，本来二位上 0 + 1 没有产生进位，但是由于个位上两个 1 相加产生了进位，导致现在二位上其实是 0 + 1 + 1，由此产生了进位，这种情况我们称之为传播，用 $P_i$ 表示第 i 位是否传播，不难发现， $A_i$ 和 $B_i$ 只要有一个为 1，第 i 位就会传播，所以 $P_i=A_i + B_i$ （ $A_i + B_i$ 表示 $A_i$ 和 $B_i$ 做「或」操作）。

下表展示了 A 和 B 相加时第 i 位上生成和传播的各种情况（别忘了， $C_i$ 代表第 i - 1 位产生的进位）：

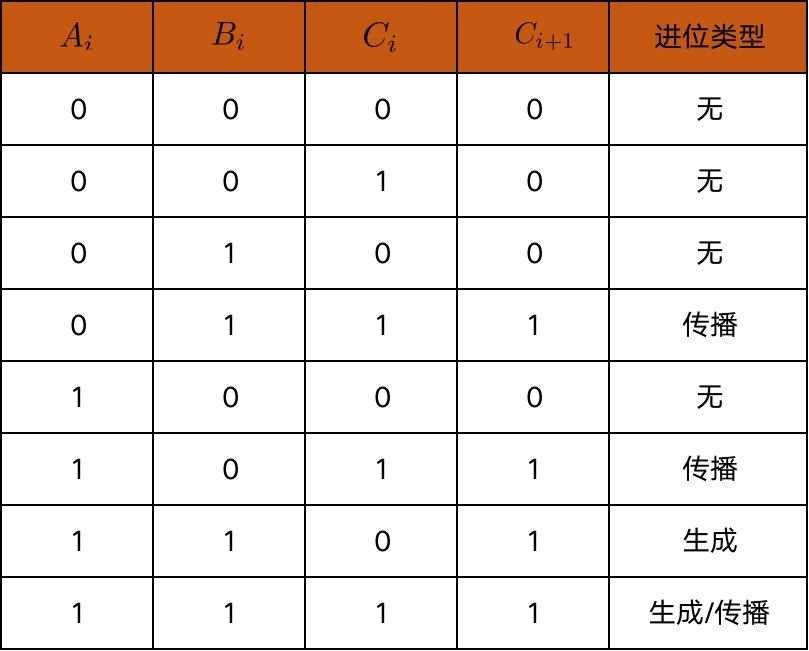
生成和传播决定了 A、B 相加时某一位上会不会产生进位，即 $C_{i+1}=G_i+P_i \cdot C_i$ 。例如，两个 4 bit 位的数相加时，我们可以得到以下等式：

$$C_{1}=G_{0}+P_{0}\cdot C_{0} \\ C_{2}=G_{1}+P_{1}\cdot C_{1} \\ C_{3}=G_{2}+P_{2}\cdot C_{2} \\ C_{4}=G_{3}+P_{3}\cdot C_{3} \\$$

把 $C_1$ 代入 $C_2$ ， $C_2$ 代入 $C_3$ ， $C_3$ 代入 $C_4$ ，可以得到下面这个展开的等式：

$$\begin{align*} &C_{1}=G_{0}+P_{0}\cdot C_{0} \\ &C_{2}=G_{1}+G_{0}\cdot P_{1}+C_{0}\cdot P_{0}\cdot P_{1} \\ &C_{3}=G_{2}+G_{1}\cdot P_{2}+G_{0}\cdot P_{1}\cdot P_{2}+C_{0}\cdot P_{0}\cdot P_{1}\cdot P_{2} \\ &C_{4}=G_{3}+G_{2}\cdot P_{3}+G_{1}\cdot P_{2}\cdot P_{3}+G_{0}\cdot P_{1}\cdot P_{2}\cdot P_{3}+C_{0}\cdot P_{0}\cdot P_{1}\cdot P_{2}\cdot P_{3} \\ \end{align*}$$

因为 $G_i$ 和 $P_i$ 都是由 $A_i$ 和 $B_i$ 计算出来的，并且 $C_0=0$ ，所以 $C_1\sim C_4$ 都可以直接通过电路算出来，无需等待前面的计算结果，得到 $C_i$ 之后，再将$C_i$与$A_i$、$B_i$输入全加器，即可得到每一位上的计算结果。与原始的全加器从右往左依次计算相比，CLA 效率要高很多。

由于 CLA 的电路实现比较复杂，且位数越多越复杂，所以一般以 4 个全加器为一组，组成一个 CLA，再将多个 CLA 组合起来，组成超级 CLA，实现多位二进制数的加法运算。

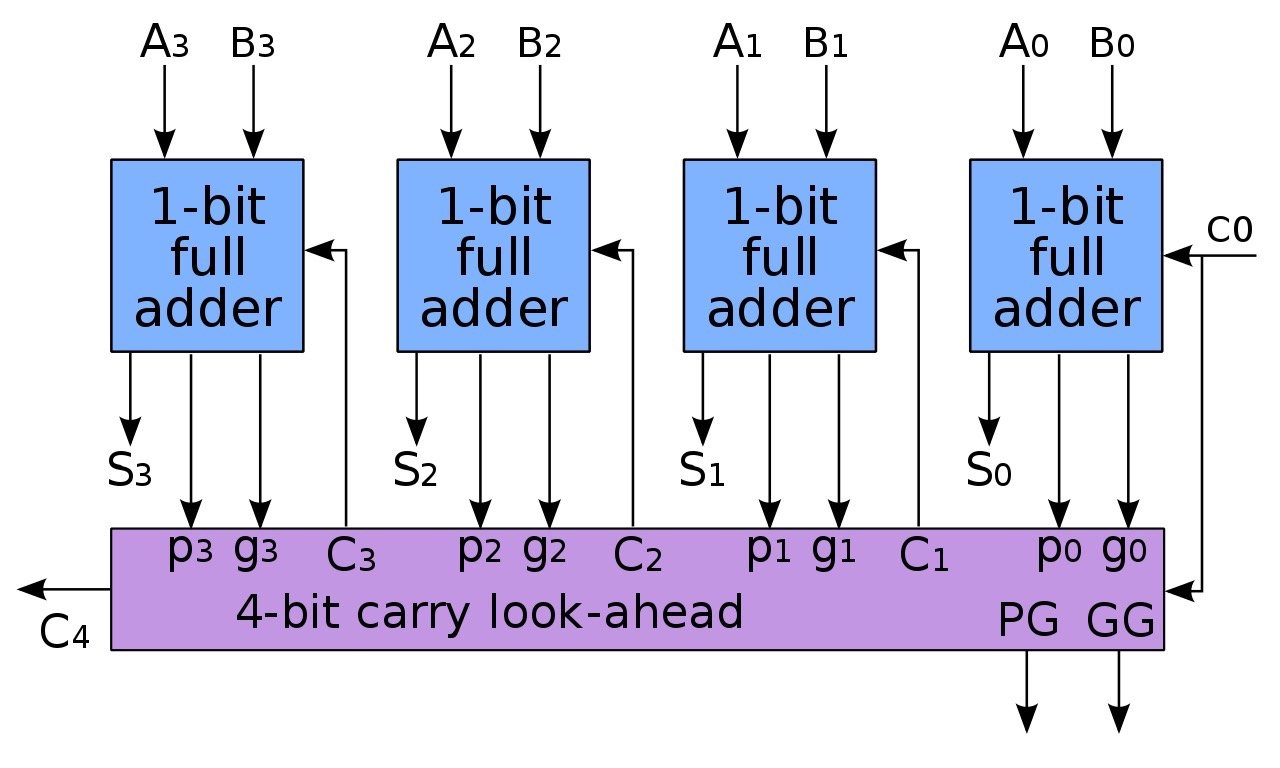
在 CLA 的基础上，又进一步演化出了曼彻斯特进位链，低位可以共享高位的逻辑电路，计算当前位的进位，节省了电路数量。

下面是用 Java 模拟的超前进位加法器的计算过程。

package com.supermouse;

import java.util.Objects;

/**
 * 模拟超前进位加法器的计算过程
 * @author 王浩
 * @date 2020/12/16
 */
public class TestCLA {
    private static int p(int a, int b) {
        return a | b;
    }

    private static int g(int a, int b) {
        return a & b;
    }

    private static String arrayToString(int[] arr) {
        if (Objects.isNull(arr) || arr.length == 0) {
            return "";
        }
        StringBuilder sb = new StringBuilder();
        for (int value : arr) {
            sb.append(value);
        }
        return sb.toString();
    }

    private static int binaryToDecimal(int[] arr) {
        if (Objects.isNull(arr) || arr.length == 0) {
            return 0;
        }
        int sum = 0;
        int digit = 0;
        for (int i = arr.length - 1; i >= 0; i--) {
            sum += (1 << digit++) * arr[i];
        }
        return sum;
    }

    public static void main(String[] args) {
        // 参与计算的数的位数
        final int bitLength = 4;
        int[] A = new int[bitLength];
        int[] B = new int[bitLength];
        int[] C = new int[bitLength + 1];
        int[] S = new int[bitLength + 1];
        // int a = 8, b = 6;
        out: for (int a = 0; a < (1 << bitLength); a++) {
            for (int b = 0; b < (1 << bitLength); b++) {
                int originA = a, originB = b;
                // 把十进制转成二进制
                for (int i = bitLength - 1; i >= 0; i--) {
                    A[i] = originA % 2;
                    B[i] = originB % 2;
                    originA /= 2;
                    originB /= 2;
                }
                System.out.println("A：" + a + "，二进制：" + arrayToString(A));
                System.out.println("B：" + b + "，二进制：" + arrayToString(B));
                // 以下4步在硬件层面可以通过电路同时计算
                C[3] = g(A[3], B[3]) | (p(A[3], B[3]) & C[4]);
                C[2] = g(A[2], B[2]) | (p(A[2], B[2]) & C[3]);
                C[1] = g(A[1], B[1]) | (p(A[1], B[1]) & C[2]);
                C[0] = g(A[0], B[0]) | (p(A[0], B[0]) & C[1]);
                // 这个循环在硬件层面可以通过电路同时计算
                for (int i = bitLength - 1; i >= 0; i--) {
                    S[i + 1] = A[i] ^ B[i] ^ C[i + 1];
                }
                S[0] = C[0];
                int calculateResult = binaryToDecimal(S);
                System.out.println("计算结果：" + calculateResult + "，二进制：" + arrayToString(S));
                if (calculateResult != a + b) {
                    System.out.println("计算错误！！！");
                    break out;
                }
                System.out.println();
            }
        }
    }
}

参考资料：

• https://time.geekbang.org/column/article/95883

• https://en.wikipedia.org/wiki/Carry-lookahead_adder

本文部分图片来自网络，如有侵权，请联系作者删除

发布时间：2020 年 12 月 20 日